Teorema de Pitágoras

maio 10, 2023

Teorema de Pitágoras

Teorema de Pitágoras relaciona o comprimento dos lados do triângulo retângulo. Essa figura geométrica é formada por um ângulo interno de 90°, chamado de ângulo reto.

O enunciado desse teorema é:

"A soma dos quadrados de seus catetos corresponde ao quadrado de sua hipotenusa."

Fórmula do teorema de Pitágoras

Segundo o enunciado do Teorema de Pitágoras, a fórmula é representada da seguinte maneira:

a2 = b2 + c2

Sendo,

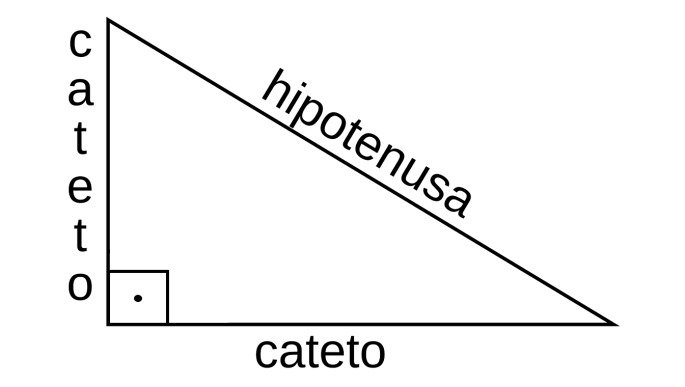
a: hipotenusa
b: cateto
c: cateto

A hipotenusa é o maior lado de um triângulo retângulo e o lado oposto ao ângulo reto. Os outros dois lados são os catetos. O ângulo formado por esses dois lados tem medida igual a 90º (ângulo reto).

Identificamos ainda os catetos, de acordo com um ângulo de referência. Ou seja, o cateto poderá ser chamado de cateto adjacente ou cateto oposto.

Quando o cateto está junto ao ângulo de referência, é chamado de adjacente, por outro lado, se está contrário a este ângulo, é chamado de oposto.

Veja a seguir três exemplos de aplicações do teorema de Pitágoras para as relações métricas de um triângulo retângulo.

Exemplo 1: calcular a medida da hipotenusa

Se um triângulo retângulo apresenta 3 cm e 4 cm como medidas dos catetos, qual a hipotenusa desse triângulo?

$reto a ao quadrado espaço igual a espaço reto b ao quadrado espaço mais reto c ao quadrado reto a ao quadrado espaço igual a espaço 4 ao quadrado espaço mais espaço 3 ao quadrado reto a ao quadrado espaço igual a 16 espaço mais espaço 9 reto a ao quadrado espaço igual a 25 reto a espaço igual a espaço raiz quadrada de 25 reto a espaço igual a espaço 5$

Portanto, os lados do triângulo retângulo são 3 cm, 4 cm e 5 cm.

Exemplo 2: calcular a medida de um dos catetos

Determine a medida de um cateto que faz parte de um triângulo retângulo, cuja hipotenusa é 20 cm e o outro cateto mede 16 cm.

$reto a ao quadrado espaço igual a espaço reto b ao quadrado espaço mais reto c ao quadrado espaço seta dupla para a direita reto b ao quadrado espaço igual a espaço reto a ao quadrado espaço menos espaço reto c ao quadrado reto b ao quadrado espaço igual a espaço 20 ao quadrado espaço menos espaço 16 ao quadrado reto b ao quadrado espaço igual a espaço 400 espaço menos espaço 256 reto b ao quadrado espaço igual a 144 reto b espaço igual a espaço raiz quadrada de 144 reto b espaço igual a espaço 12$

Portanto, as medidas dos lados do triângulo retângulo são 12 cm, 16 cm e 20 cm.

Exemplo 3: comprovar se um triângulo é retângulo

Um triângulo apresenta os lados com medidas 5 cm, 12 cm e 13 cm. Como saber se é um triângulo retângulo?

Para provar que um triângulo retângulo é verdadeiro as medidas dos seus lados devem obedecer ao Teorema de Pitágoras.

$reto a ao quadrado espaço igual a espaço reto b ao quadrado espaço mais espaço reto c ao quadrado 13 ao quadrado espaço igual a espaço 12 ao quadrado espaço mais espaço 5 ao quadrado 169 espaço igual a espaço 144 espaço mais espaço 25 169 espaço igual a 169$

Como as medidas dadas satisfazem o teorema de Pitágoras, ou seja, o quadrado da hipotenusa é igual a soma do quadrado dos catetos, então podemos dizer que o triângulo é retângulo.

Triângulo Pitagórico

Quando as medidas dos lados de um triângulo retângulo são números inteiros positivos, o triângulo é chamado de triângulo pitagórico.Neste caso, os catetos e a hipotenusa são denominados de “terno pitagórico” ou “trio pitagórico”. Para verificar se três números formam um trio pitagórico, usamos a relação a2 = b2 + c2.

O mais conhecido trio pitagórico é representado pelos números: 3, 4, 5. Sendo a hipotenusa igual a 5, o cateto maior igual a 4 e o cateto menor igual a 3.

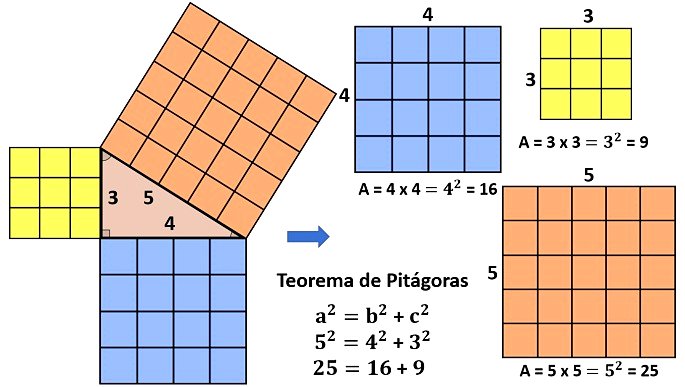
Observe que a área dos quadrados desenhados em cada lado do triângulo relacionam-se tal como o teorema de Pitágoras: a área do quadrado no lado maior corresponde à soma das áreas dos outros dois quadrados.

É interessante notar que, os múltiplos desses números também formam um terno pitagórico. Por exemplo, se multiplicarmos por 3 o trio 3, 4 e 5, obtemos os números 9, 12 e 15 que também formam um terno pitagórico.

Além do terno 3, 4 e 5, existe uma infinidade de outros ternos. Como exemplo, podemos citar:

5, 12 e 13
7, 24, 25
20, 21 e 29
12, 35 e 37

Quem foi Pitágoras?

Segundo a história Pitágoras de Samos (570 a.C. - 495 a.C.) foi um filósofo e matemático grego que fundou a Escola Pitagórica, localizada no sul da Itália. Também chamada de Sociedade Pitagórica, incluía estudos de Matemática, Astronomia e Música.

Embora as relações métricas do triângulo retângulo já fossem conhecidas pelos babilônicos, que viveram muito antes de Pitágoras, acredita-se que a primeira demonstração que esse teorema se aplicava a qualquer triângulo retângulo tenha sido feita por Pitágoras.

O Teorema de Pitágoras é um dos teoremas mais conhecidos, importantes e utilizados na matemática. Ele é imprescindível na resolução de problemas da geometria analítica, geometria plana, geometria espacial e trigonometria.

Além do teorema, outras importantes contribuições da Sociedade Pitagórica para a Matemática foram:

Descoberta dos números irracionais;
Propriedades dos números inteiros;
MMC e MDC.
Demonstrações do Teorema de Pitágoras
Existem diversas formas de provar o teorema de Pitágoras. Por exemplo, o livro The Pythagorean Proposition, publicado em 1927, apresentava 230 formas de demonstrá-lo e uma outra edição, lançada em 1940, aumentou para 370 demonstrações. Assista o vídeo e confira algumas demonstrações do Teorema de Pitágoras.
Assista o vídeo a seguir e confira algumas demonstrações do Teorema de Pitágoras.
Fonte:Teorema de Pitágoras: fórmula e exercícios - Toda Matéria (todamateria.com.br)

Pesquisar este blog

CONHECENDO A MATEMATICA